世界は数学で満ちている『世界を変えた17の方程式』

数と数の関係性を明らかにして、数の意味を理解したり別の数を計算する。それが方程式の役割で、鍵となるのは = で表す等号だ。数学は記号を使った言語であり、すべて言葉に翻訳できる。方程式であれば「〜と〜は」という主語で始まり、「等しい」という述語で終わる。

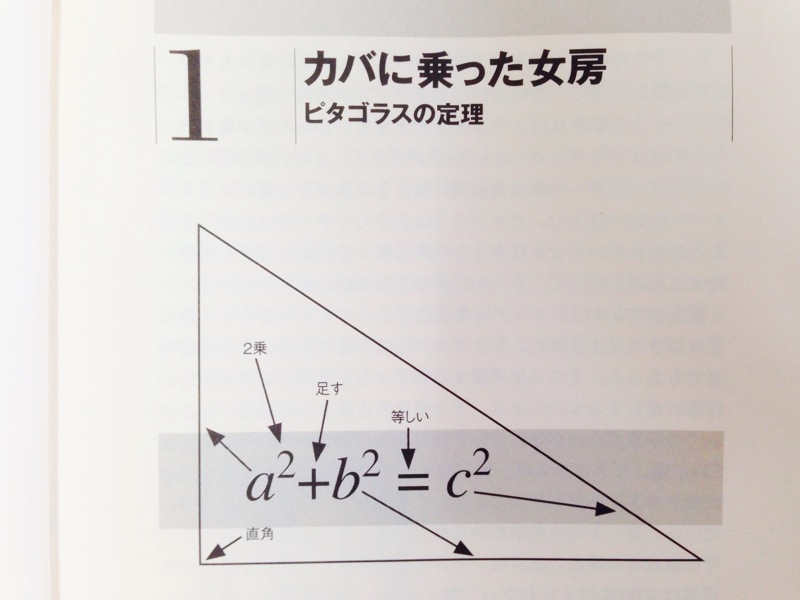
例えばアインシュタインの方程式「E=mc²」は、「物体のエネルギーは、その質量と、光の速さの2乗との積に等しい」と言葉で説明できる。ピタゴラスの定理「a²+b²=c²」なら、「直角三角形の斜辺の2乗は、隣り合った2つの辺の2乗の和に等しい」といった具合だ。

方程式には世界を変える力がある。自然の中に隠れているパターンを発見すると、科学技術のレベルが大きく飛躍する。それをドラマチックに丁寧に教えてくれるのが、数学者イアン・スチュアートによる『世界を変えた17の方程式』だ。

第1章 カバに乗った女房 ピタゴラスの定理

ピタゴラスは、直角三角形の3つの辺が互いにどのような関係にあるのか明らかにした。三角法、測量、航海術、空間・時間・重力の特殊相対論と一般相対論に発展した。

第2章 手順を短くする 対数

ネイピアは、数を足すことが数を掛ける代わりになることを突き止めた。天体現象の効率的な計算、計算尺、放射性崩壊の解明、知覚の物理学に発展した。

第3章 消えゆく量の亡霊 微積分

ニュートンは、傾きや面積の計算法と、立体の体積や曲線の長さの公式を発見した。高層建造物、車、飛行機、携帯電話、宇宙ロケットの開発、地震の震動、サスペンションの上下運動、細菌の増殖時間の計算に応用されている。

第4章 世界の体系 ニュートンの重力の法則

ニュートンは2つの物体の間に働く重力を、質量と距離に基づいて決定した。天体の食、惑星の軌道、彗星の回帰、銀河の回転予測、人工衛星、地球の計測、ハッブル宇宙望遠鏡、太陽フレアの観測、惑星探査機、衛星通信、全地球測位システムに発展。

第5章 理想世界の兆し マイナス1の平方根

ガウスは、数iの2乗はマイナス1である事を明らかにして、複素解析を生み出した。三角関数を計算する方法。波、熱、電気、磁気を理解する方法、量子力学の数学的基礎、電気照明、デジタルカメラに応用。

第6章 結び目をめぐる騒ぎ オイラーの多面体の公式

オイラーは、立体の面、稜、頂点の数は互いに独立しておらず、単純な形で関連していることを明らかにした。細胞中で酵素がどのようにしてDNAに作用するか、天体の運動がなぜカオス的なのかを理解する基礎となった。

第7章 偶然のパターン 正規分布

モアブルは、ある特定のデータの値が観測される確率が、平均値の近くでもっとも大きく、平均との差が大きくなるにつれて急速に下がっていくことを突き止めた。統計学や医学臨床試験などの実験結果の有意性を調べるテストに発展。

第8章 良い振動 波動方程式

タランベールは、バイオリンの弦が波を作って運動することを予測し、水の波、音波、光の波、弾性振動を一般化した。地球内部の構造解析、原油の採掘、ラジオ、テレビ、レーダー、通信技術、津波警報システムに発展。

第9章 さざ波とパルス フーリエ変換

フーリエは、空間と時間におけるすべてのパターンが、それぞれ異なる振動数を持つサイン関数のパターンと重なることを発見した。DNAの解明、画像データの圧縮（JPEG）、劣化した古い音声記録の再現、地震の解析、指紋データの効率的な保管、医療用スキャナーの性能向上に応用。

第10章 人類の飛翔 ナヴィエ＝ストークス方程式

ナヴィエとストークスは、流体運動の計算方法を明らかにした。旅客機、潜水艦、F1カーの開発、血管内の血液の流れ、コンピュータの計算流体力学に発展。

第11章 エーテルのなかの波 マクスウェル方程式

マクスウェルは、電場の回転がその回転面と垂直方向に磁場を作り、磁場の回転がその回転面と垂直方向・逆向きに電場を作る事を発見した。ラジオ、レーダー、テレビ、コンピュータ機器のワイヤレス接続、および現代の通信の大部分が誕生した。

第12章 法則と無秩序 熱力学の第2法則

ボルツマンは、熱力学系の無秩序の程度がつねに増大することを突き止めた。蒸気機関、再生可能なエネルギーの効率の評価、「宇宙の熱的死」のシナリオ、物質が原子からできていることの証明に応用された。

第13章 絶対であるのは1つだけ 相対論

アインシュタインは、物体のエネルギーが、その質量と、光の速さの2乗との積に等しいことを発見した。光の速さはきわめて大きく、その2乗はとてつもなく巨大だ。核兵器、ブラックホール、ビックバン、GPS、衛星ナビゲーションに発展した。

第14章 量子の不気味さ シュレディンガー方程式

シュレディンガーは、物質を粒子としてではなく波としてモデル化し、その波がどのように伝わるかを記述した。きわめて小さなスケールの世界の物理学を劇的に変えた。コンピュータチップやレーザー、CD、測量、天文学、外科技術、ミサイルに応用。

第15章 暗号、通信、コンピュータ 情報理論

シャノンは、1つのメッセージに含まれている情報量を、記号が出現する確率に基づいて定義した。デジタル通信　電話、CD、DVD、インターネット、宇宙探査機、統計学、人工知能、暗号学、DNA配列の解析に応用。

第16章 自然のアンバランス カオス理論

スメールとアルノートリは、生物の個体数が世代ごとにどのように変化するかをモデル化し、その見かけのランダムさの裏に秩序が隠されていることを明らかにした。太陽系の惑星の運動、気象予報、生態系の個体数、ダイナミクス、変更量、地震のモデル化、宇宙探査機の効率的な軌道に応用。

第17章 ミダスの数式 ブラック＝ショールズ方程式

ブラックとショールズは、金融派生商品の価格が時間とともにどのように変化するか明らかにした。それにより金融部門が大きく成長し、経済が大きく繁栄した末に、経済恐慌、1990年代の株式市場の混乱、2008年から2009年までの金融危機、それに続く経済不況が起こった。

最も興奮したのは、第4章に登場する日本の宇宙探査機「ひてん」の話。月の測量を終えて燃料がほとんど尽きていたにもかかわらず、方程式を使って最も効率の良い軌道を設計し直し、延命したそうだ。

方程式には負の側面もある。方程式をもとに核爆弾が開発され、経済の金融危機が起こった。だが、方程式がなければテレビやスマートフォン、照明や電子レンジ、車や衛星ナビゲーションなど、今ある製品や技術は存在しない。

『世界を変えた17の方程式』は、私たちの身の回りに方程式が満ちていることを教えてくれる。

➤ 世界を変えた17の方程式（ソフトバンククリエイティブ）Amazon / Kindle / 楽天ブックス / 楽天kobo

関連記事

• 『情報技術の人類史』を読まずして未来を生きるなかれ - #RyoAnnaBlog
• 世界は数学でできている『数学する本能 』 - #RyoAnnaBlog
• 自分の限界を突破するための本 6選 - #RyoAnnaBlog